律制

应Scateu的邀请，打算把之前在乐队讲课的一些东西放上来。然而回头看了看，讲了七八年，却并没有留下什么文字的资料。罢了，都已经答应了，就现写一点儿吧。

这一篇，我们写写律制。律制这个东西听起来很玄妙，换个名字也许更好理解些，叫作“音乐的数学基础”好了。

自打接触音乐开始，我就一直在思考一个问题：为什么东西方的音乐，两个之前几乎完全没有交集的体系，居然发展出了完全相同的音阶？为什么中国的古曲居然都可以直接在五线谱上标记出来？如果理性地不认为这是一种冥冥之中的巧合，那一定有某种放之四海而皆准的力量在左右人们对于声音的理解。这种力量是如此强大，以至于在如此不同的人们那里——语言、文字、道德、宗教的差异充分说明了人类能有多么不同——都获得了完全的认同。这是一种纯粹的、绝对客观的力量。

我想，这也是为什么中国人将其称之为“律”。“定律”、“规律”、“法律”，神圣而至高无上的规则。这是什么？这是数学。

古人很早就发现了，中空的管子能够发出固定音调的声音，不同长度的管子音调不一样。骨制和陶制排箫的出土充分说明了这一点。但是中国最早见诸于典籍的有关律制的研究，应该是在春秋时代，《管子 地员篇》和《吕氏春秋 音律篇》中，分别记载了用于生成音阶的方法。这个故事大概是这样的： 中国古代的青铜器冶炼技术比较发达，既然到了西周都已经有了编钟这种比较变态的乐器，铸造一个中空的铜管子应该不是什么难事。管子造出来之后，有人上去敲了一下，铜管发出了悦耳的”咚~”的一声。动作难度不算高，但是大有讲究。物理上说，铜管受到一个时间趋近于零的冲击，其响应应该叫做这个系统的“冲激响应”，而这个冲激响应的频率，就是这个铜管固有的谐振频率。其实现代也有靠敲铜管演奏音乐的乐器，就叫作管钟（TUBULAR BELLS）。古人觉得这个声音很好听，就给这个音起了个名字，铜做的管子，嗯，就叫“黄钟”好了。

有了这么根好玩的铜管子，好奇的人类总会去想折腾一下它。于是有人想到，我们把管子截短一半，会怎么样？一半长度的管子发出了另一个声音。从我们今天的认识上看，半长管子的谐振频率应该是原来管子的两倍，在现代音乐体系里面，这个音比之前那个音高了八度，音名应该是一样的。古人也天才地觉得这两个音其实应该算是一个音，可能是因为发现两个音如果同时发出，是可以完全叠在一起的（此处立一个flag，有关音色的问题我再写一篇吧），所以并没有给它再起一个名字。继续按照一半一半地去截好像没有什么大的意义了，不如，我们截它三分之一试试？

这一试可不得了，截出了一个伟大的发明。长度为$\frac{2}{3}$的管子，其谐振频率为原来的1.5倍，一个新的音出现了。在现代音乐体系里面，这个音和原来那个音成纯五度关系，如果认为“黄钟”是C，那么这个音就是G。古人认为这个音很好，因为它和原来的那个音叠在一起非常和谐，于是将这个音命名为“林钟”。为什么和谐呢？这个真的是可以算的：

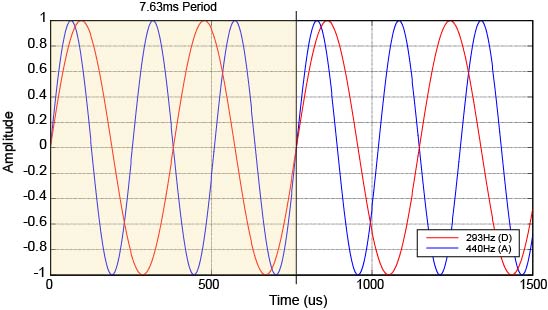
古人耳中“黄钟”的频率现在是没法知道了，我们假设它和现在的中央C一样高吧，大概在262Hz左右。那么“林钟”的频率，大概会在392Hz上下。无论怎样，因为“林钟”的频率是“黄钟”的1.5倍，那么三个“林钟”的周期和两个“黄钟”的周期是正好重叠的，算来这样的大周期大概不到8个毫秒。视觉有暂留，听觉也难以分辨出这么块的重复周期，于是就把它当成一个整体来处理了。换句话说，这两个音的叠加产物被耳朵认为是“有规律振动的产物”，属于“乐音”，是“和谐的”。

把管子截短$\frac{1}{3}$叩开了新世界的大门，古人当然不会止步于此。按照现代音乐体系，从C（黄钟）开始五度五度地往上数，中国的古人依次创造了G（林钟），D（太簇），A（南吕），E（姑洗）。说到这里打断一下，这五个音有点特别。大家会发现中国的曲子，从《春江花月夜》到《北京欢迎你》，很多都只有CDEGA这五个音。这五个音古称“宫商角徵羽”，构成了中国的五声音阶。当然这么截下午管子会越来越短，操作起来不太容易，不过既然认为延长一倍是同一个音，这个问题也不难解决。继续往上数，E后面应该是B（应钟），然后就是$\sharp$ F（蕤宾）。如果大家喜欢听京剧，会发现京剧曲调中很多使用到$\sharp$ F，我想很可能也和这个有关系。$\sharp$ F再往上，是$\sharp$ C（大吕），$\sharp$ G（夷则），$\sharp$ D（夹钟），$\sharp$ A（无射），$\sharp$ E（仲吕，一作中吕），然后是…

等等。$\sharp$ E往上应该是$\sharp$ B，耳朵很好的古人们发现了，这个音和C非常接近，既然如此，继续生成下去，后面的每个音都会和前面已经有的音很接近。那么，不如就在这里闭合，形成循环吧。这种靠$\frac{1}{3}$的截短（也包括延长）产生音阶的方法，称之为“三分损益法”，由于其生成的音两两相差五度，基于这样方法的律制被称之为“五度相生律”。

然而问题就出现了。如果要形成循环，这个$\sharp$ B应当等于C。然而，数学告诉我们，因为三分损益法生成的音律频率中有3的因数，而不同组的C之间的频率的倍数一定是$2^{n}$，所以无论如何二者都不可能相等，总有那么一点点差异。这个差异是：

这个问题在中国，被称之为“仲吕上生不及黄钟”，就是$\sharp$E再升五度，管子比黄钟要短那么一点点（频率高一点点）。看起来好像差别也不太大么，百分之一多一点，值得这么认真么？数学上给人的感觉并不直观，听一听会发现，其实差别还挺大的。这个差异被称之为“古代音差”或者“最大音差”，很显然，数学上可以证明，它是不可能在五度相生律范畴内解决的。

聪明人全世界都有，三分损益法在西方也很早就被发现了，发现的人就是赫赫有名的古希腊数学家Πυθαγόρας。注意，这不是一个公式，照着认识的希腊字母念下来，大概也能猜到“毕达哥拉斯”的大名。这位姓Π的高手是一个著名的有理数狂人，认为天下所有的数都可以用自然数的比来表示。这么喜欢比例，他发现频率的比例关系自然并不让人意外。毕达哥拉斯似乎使用琴弦来按比例生律的，这个确实比铜管子要方便一些，至少可以很轻松地延长。所以一开始，西方的音律就向两个方向同时展开了。C向下五度，第一个就生成了F，大概这就是在中国（汉民族）传统音乐里一直不太受待见的F早早成为了西方七声音阶一员的原因吧。当然，毕达哥拉斯也遇到并提到了最大音差问题，所以西方称这个问题为“毕氏音差”。相似的命名还有“毕达哥拉斯定理”，也就是中国的勾股定理。

捎带一提，毕达哥拉斯对有理数的执着带给了他很多成就，但也因此禁锢了他的脚步。他的学生希帕索斯发现用他的定理算出的$\sqrt{2}$——边长为1的等腰直角三角形的斜边长度——没有办法表示成自然数之比，这个“以子之矛攻子之盾”的发现惹怒了毕达哥拉斯学派，最终让希帕索斯葬身大海。所以，当你的论文被学术门派不同的审稿人拒了的时候也不要太沮丧，毕竟人家并没有赶过来除掉你这个异端么。

说回音乐。总结一下，五度相生律的最大优势是，律制中的大部分音，频率之比都比较简单。从我们之前的讨论来看，这意味着同时演奏几个音的时候，其和声会比较和谐。当然，（类）小二度之类的和弦，两个音的频率比例比较复杂，其混合产物的周期太长，于是耳朵还是会拒绝认为这是一个和谐的乐音。五度相生律最大的缺点，就是由于“最大音差”的存在，如果需要形成完整的音阶，需要以某种方式进行一些妥协。

为了弥合“最大音差”，古人也是想了很多的办法。其中最著名的解决方案，莫过于“平均律”。

听起来高大上，说起来很简单。五度相生律生成的音阶告诉了我们两件事情：第一，相差八度的两个音，频率差是两倍，因此音名是相同的（比如都是C）；第二，相差八度的两个音（比如相差八度的两个C），之间一共能塞下11个音（$\sharp$ C，D，$\sharp$ D，E，F，$\sharp$ F，G，$\sharp$ G，A，$\sharp$ A，B），从五度相生律上来看，相邻两个音的频率比例好像挺接近。Hmmm… 很接近？让他们都相等不好么？

平均律就是这么来的，简直简单粗暴。从一个基准音（比如C）开始，每一个半音，其频率都是前一个音频率的$2^{\frac{1}{12}}$倍，那么12个半音程之后，频率变成了基准音的$(2^{\frac{1}{12}})^{12}$倍（就是两倍呀！），正好高一个八度。打完收功，天下太平。频率的比例基数是二的十二次方根！不知道毕达哥拉斯听到这么个数会不会气活过来。

提到十二平均律大家估计都会首先想到巴赫，不过真要查起书来，第一份有关这个的文献还是来自于中国，这个人是明朝人，叫作朱载堉。对历史比较敏感的人会立刻意识到这个人来头绝对不小，毕竟在明朝敢姓朱，第三个字儿还是金木水火土偏旁的一定不是一般人。好在这位皇太祖九世孙没什么机会也并不喜好参与皇族的纷扰，唯独喜欢钻研音律和数学，写了不少paper，成为了一名重量级科学家，然后太平地活了76岁。朱氏使用81档之超级大算盘计算了$2^{\frac{1}{12}}$，“有效数字多达25位”，并（首次）提出了十二平均律的理论。西方有文献记载的最早的相关文章，在此之后数十年。虽然本人并不认同很多资料所述“西方的平均律理论是受到朱载堉发明的影响”，但朱载堉本身的成就绝对是应当是得到认同的。

当然光发明了并没有什么（雾）用，成功与否还得看市场推广。朱的研究在中国一直被束之高阁，可能连他自己也并没有意识到这个发明有什么大用，回头接着算别的事情去了。但是西方，十二平均律的粉丝中正好有个前无古人后无来者的作曲家——约翰·塞巴斯蒂安·巴赫。巴赫在1722和1744年分别写了两卷《十二平均律曲集》，每卷含有一整套24首前奏曲和赋格。曲子怎么样我觉得以我的欣赏水平没有资格评价，但这两卷《十二平均律曲集》充分体现了十二平均律的音乐效果，并且在后世广为流传，甚至被称为“钢琴演奏的旧约全书”，被无数钢琴家学习和练习。有空还是建议有兴趣的同学好好听听。这个故事告诉我们，概念是一方面，没有好产品，市场照样不接受啊。

那么总结一下十二平均律。十二平均律首要的价值在于它解决了“最大音差”的问题，实际上这也是这种律制出现的契机；其次，平均律中每两个音之间频率的比例关系是固定的，这意味着半音的位置很固定，比如$\sharp$ C和$\flat$ D，两个音在平均律中是等音，这为键盘乐器提供了很大的方便，并且使得转调非常容易。平均律的缺点也很突出，由于$2^{\frac{1}{12}}$是个彻底的无理数，一个八度内的任意两个音的频率比例都不是简单整数，甚至都不是有理数。这意味着实际上，（除了八度外）任何平均律内的和弦都是“不准”的，而这种“不准”是能够被部分耳朵灵敏的人捕捉到的。因此，平均律有的时候也被（开玩笑地）称之为“不准率”。

两种比较主要的律制讲完了。实际上，现在还有一个经常听到的名词叫作“纯律”。说实在的本人对纯律并不熟悉，但是从数学的角度来说，还是挺好理解的。五度相生律中，相邻四个半音（也就是现代音乐里的大三度）的频率比例是$\frac{(\frac{3}{2})^4}{2^4} = \frac{81}{64}$。注意，这个音实在很接近$\frac{5}{4}$，但是稍稍了一点儿。太可惜了，不如直接改成$\frac{5}{4}$吧？这样会让大三度听起来更和谐，而且（因为降低了大三度跨度，一定程度上）可能改善“仲吕上生不及黄钟”的问题。加入了大三度$\frac{5}{4}$的生率方法，就是纯律。欸？$\frac{2}{3}$是五度相生率，加入$\frac{4}{5}$是纯律，中间好像少了点什么，$\frac{3}{4}$哪里去了？哈，$\frac{3}{4}$就是$\frac{3}{2}$再除以2（降八度）嘛。

纯律的优缺点和五度相生律类似，因为大部分两个音频率之比是简单自然数，所以和弦听起来十分和谐。但是同样由于整数比的关系，同是相差一个半音，在不同位置的频率比却并不相同，这为转调带来了很大的困难。另外，由于生律的方向并不相同，在十二平均律下的某些等音，例如$\sharp$ G和$\flat$ A，在纯律/五度相生律中却并不相等。这不行啊，这怎么做钢琴啊？总不能在G和A两个白键之间插上两个黑键吧。

三种主要的律制说得差不多了，孰优孰劣，本人这种业余玩票的工科男就实在没有资格评判了。在这里说说我自己的理解。感觉上，五度相生律规整方正，音程和谐，本人接触较多的民族音乐和民歌中应用较多，似乎比较适合单音序列式的音乐。民乐中的很多乐器都是以五度相生律来定弦的。纯律更加偏重保证和弦的和谐，在多声部，若干个/乐器同时演奏时，优势最为明显。但是由于音阶频率比例的不平衡相较五度相生律更为明显，如果用来演奏一个单一声部的音符序列，细听起来总有些“怪怪的”。按我的理解，室内乐例如弦乐四重奏这样形式的音乐中，纯律会很有用途。平均律是一个数学严格的折衷方案，绝对适合键盘乐器，例如钢琴。这一点就不用多说了。

说得似乎很严格，我想在实际应用中，并不会严格按照某一种律制体系进行，总是会有些妥协和变通的。对于弦乐的演奏者来说，很有可能在不同时候拉同一个音，频率并不完全相同——在和其他声部和弦时用纯律，而solo的乐段用五度相生律。个中的差异，只在手指动作的微微变化，妙不可言。当年在乐队的时候，指挥常常说要听着其他声部的声音演奏，我想也许就是这个道理。也许演奏者本身并不能具体描述出这种区别，但是耳朵永远是正确的。而钢琴这样的乐器，音准实际是由调音师控制的。虽然我们都说钢琴是一种平均律乐器，但是实际操作时调音师也往往并不会按照严格的平均律频率去调琴，而更多地信赖自己的耳朵。调琴常用的四五度调律法和三六度调律法，实际上是通过对成比例音程的细微调整去逼近平均律，其最后的结果也应当是介于平均律和相生律之间吧。